毫米波(mmWave)属于一种特殊的雷达技术,其运用短波长电磁波。雷达系统发射的电磁波信号在其发射路径上若被物体阻挡,便会发生反射。通过捕获反射信号,雷达系统能够确定物体的距离、速度和角度。
毫米波雷达可发射毫米量级波长的信号。在电磁频谱中,此波长被视作短波长,这也是该技术的优势所在。确实,处理毫米波信号所需的系统组件(如天线)尺寸极小。短波长的另一优势是具有高准确度。工作频率为 77–81GHz(对应波长约为 4 毫米)的毫米波系统,能够检测小至零点几毫米的移动。
完整的毫米波雷达系统涵盖发送(TX)和接收(RX)射频(RF)组件、时钟等模拟组件,以及模数转换器(ADC)、微控制器(MCU)和数字信号处理器(DSP)等数字组件。过去,这些系统都是通过分立式组件来实现的,这导致了功耗增加和总体系统成本上升。
全球可提供雷达芯片的厂商:德州仪器(Texas Instruments,简称 TI)、意法半导体(STMicroelectronics)、恩智浦半导体公司(NXP Semiconductors)、博世(Bosch)、富士通(Fujitsu)等厂商,同时近几年也有多家国内厂商提供雷达相关芯片(在快速成长中)。
距离测量
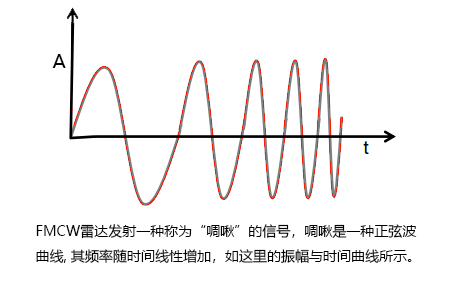
(图1)
图 1 线性调频脉冲信号(以振幅作为时间的函数)。
图 2 FIGURE 1 & 2为同一个线性调频脉冲信号(频率作为时间的函数)。该线性调频脉冲具有起始频率(fc ) 、带宽(B)和持续时间 (Tc )。该线性调频脉冲的斜率 (S) 捕捉频率的变化率。在例子中图 2 提供的示例中,
fc = 77 GHz,B = 4 GHz,Tc = 40 μs,
S = 100 MHz/μs.
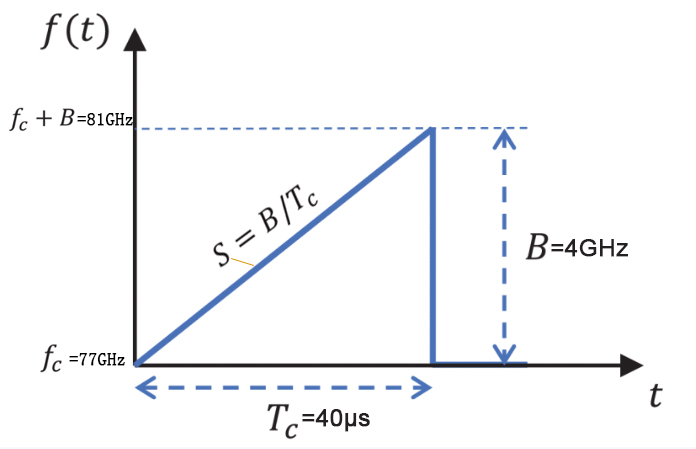
(图2)
图 2.线性调频脉冲信号(频率作为时间的函数)。
FMCW 雷达系统发射线性调频脉冲信号,并捕捉其发射路径中的物体反射的信号。图 3 所示为 FMCW雷达主射频组件的简化框图。该雷达的工作原理如下:
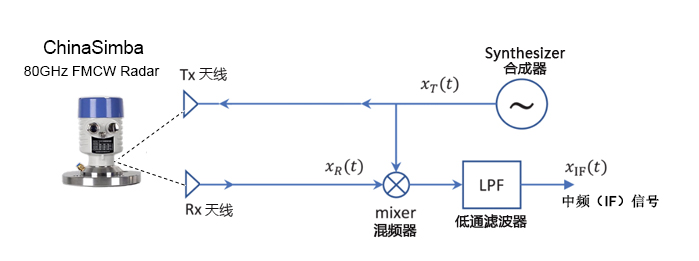
(图3)
图 3. FMCW雷达工作原理框图
• 合成器生成一个线性调频脉冲。
• 该线性调频脉冲由发射天线(TX 天线)发射。
• 物体对该线性调频脉冲的反射生成一个由接收天线(RX 天线)捕捉的反射线性调频脉冲。
• “混频器”将 RX 和 TX 信号合并到一起,生成一个中频 (IF) 信号。
混频器是一个电子组件,将两个信号合并到一起生成一个具有新频率的新信号。对于两个正弦输入 x1 和 x2(方程式 1 和 2):
𝑥1 = sin (𝜔1𝑡 + 𝛷1) (方程1)
𝑥2 = sin (𝜔2𝑡 + 𝛷2) (方程2)
输出 xout 有一个瞬时频率,等于两个输入正弦函数 的瞬时频率之差。输出 xout 的相位等于两个输入信号的相位之差(方程式 3)
𝑥out = sin[(𝜔1 − 𝜔2) 𝑡 +(𝛷1 − 𝛷2)] (方程3)
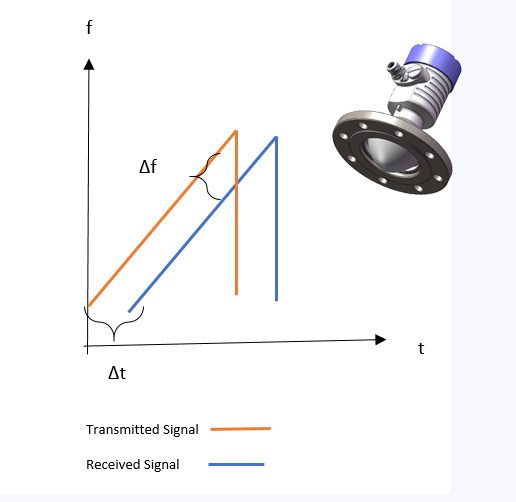
混频器的运行方式还可以以图形方式,通过观察作 为时间函数的 TX 和 RX 线性调频脉冲频率表示法来加以理解
下页图 4 中的上图为针对检测到的单个物体的 TX和 RX 线性调频脉冲作为时间的函数。请注意,该RX 线性调频脉冲是 TX 线性调频脉冲的延时版本。
延时 (t) 可通过数学方法推导出方程式 4:
𝜏 =2 𝑑/𝑐 (方程4)
其中 d 是与被检测物体的距离,c 是光速
要获取混频器输出处作为 IF 信号时间函数的频率表示法,只要去掉图 4 上半部分中显示的两条线即可。这两条线之间的距离是固定的,这表示 IF 信号包含一个频率恒定的单音信号。图 4 显示该频率为St。IF 信号仅在 TX 线性调频脉冲和 RX 线性调频脉冲重叠的时段(即图 4 中垂直虚线之间的时段)有效
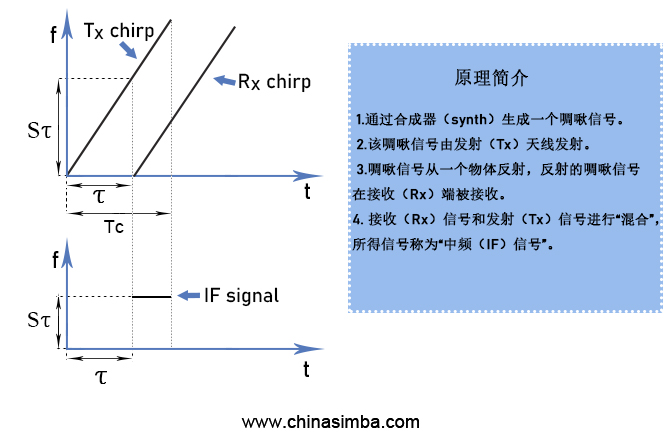
(图4)
图 4.IF频率恒定不变
混频器输出信号作为时间的幅度函数是一个正弦波,因为它有恒定频率。
IF 信号的初始相位 (F0) 是 IF 信号起点对应的时间点(即图 4 中左侧垂直虚线表示的时间点)的 TX 线性调频脉冲相位与 RX 线性调频脉冲相位之差。 (方程式 5)
𝜙0 =2𝜋𝑓𝑐t (方程式 5)
通过数学方法,它可以进一步导入方程式 6:
𝜙0 =4𝜋d/𝜆 (方程6)
总之,对于与雷达的距离为 d 的物体,IF 信号将是 一个正弦波(方程式 7),因此:
𝐴 Sin(2𝜋𝑓𝑜𝑡 + 𝜙0) (方程式 7)
其中 𝑓𝑜=S2d/ C 𝜙0 =4𝜋d/𝜆
在本介绍性白皮书中,我们忽略 IF 信号的频率与 物体速度的依赖关系。在快速 FMCW 雷达中,其 影响通常非常小,且在处理完成多普勒 FFT 后,即 可轻松对其进行进一步校正。上述分析均假设雷达 仅检测到一个物体。让我们来分析一个检测到若干 物体的情形。图 5 显示了接收自不同物体的三个不 同的 RX 线性调频脉冲。每个线性调频脉冲的延时 都不一样,延时和与该物体的距离成正比。不同的 RX 线性调频脉冲转化为多个 IF 单音信号,每个信 号频率恒定。
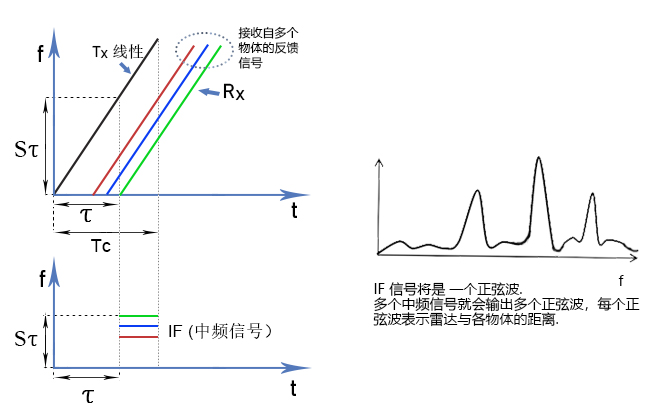
(图5)
图 5.针对多个物体检测发射的多个 IF单音信号。
* 该方程式是一个近似等式,仅在斜率和距离足够小时才有效。不过,IF信号的相位与很小的距离变化呈线性关系(即Δf=4πΔd/l)仍然是正确的。
**在本介绍性白皮书中,我们忽略 IF信号的频率与物体速度的依赖关系。在快速 FMCW雷达中,其影响通常非常小,且在处理完成多普勒 FFT后,即可轻松对其进行进一步校正。
这个包含多个单音信号的 IF 信号必须使用傅里叶变换加以处理,以便分离不同的-单音。傅里叶变换处理将会产生一个具有不同的分离峰值的频谱,每个峰值表示在特定距离处存在物体。
距离分辨率
距离分辨率即辨别两个或更多物体的能力。当两个物体靠近至特定位置时,雷达系统将无法区分这两个物体。傅里叶变换理论提出,延长中频(IF)信号能够提升分辨率。若要延长 IF 信号,需按比例增加带宽。延长后的 IF 信号会生成一个具有两个分离峰值的 IF 谱。此外,傅里叶变换理论还表明,观测窗口(T)能够分辨间隔超过 1/THz 的频率分量。这就意味着,只要频率差满足方程式 8 所给出的关系,便可以分辨两个 IF 单音信号。
Δ𝑓>1/TC (方程8)
其中 Tc 是观测时间长度。
由于Δ𝑓 = 𝑆2Δ𝑑/C , 方程式 8 可以表达为
Δ𝑑>C/2STc=C/2B
距离分辨率 (dRes) 仅取决于线性调频脉冲扫频的带宽(方程式 9):
dRes=C/2B (方程式 9)
因此,线性调频脉冲带宽为数 GHz 的 FMCW 雷达将有约为数厘米的距离分辨率(例如,4GHz 的线性调频脉冲带宽可转化为 3.75cm 的距离分辨率)